整数の分割

負でない整数 \(n\) が与えられたとき, \(n\) を正の整数の和で表すことを考えます. 例えば, 4 は

4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1

というふうに表すことができますが, これらを 4 の分割と呼びます. 整数の分割には興味深い性質があります.

Contents

厳密な定義
ヤング図形と共役な分割
母関数
オイラーの分割恒等式

厳密な定義

定義：\(n\) を負でない整数とします. 負でない整数の列 \( \lambda = (\lambda_1, \lambda_2, \lambda_3, \cdots ) \) が \( \lambda_1 \geq \lambda_2 \geq \lambda_3 \geq \cdots \) を満たし, かつ \(n = \lambda_1 + \lambda_2 + \lambda_3 + \cdots \) であるとき, \(\lambda\) を \(n\) の分割といいます. \(\lambda = (\lambda_1, \lambda_2, \lambda_3, \cdots )\) が \(n\) の分割であって, \( \lambda_{k + 1} = 0 \) のときは, \( \lambda \) を \( (\lambda_1, \lambda_2, \cdots, \lambda_k) \) と書くこともあります.

例えば, \( \lambda = (5, 4, 2) \) は 11 の分割（のひとつ）です.

定義：\(\lambda = (\lambda_1, \lambda_2, \lambda_3, \cdots )\) を \(n\) の分割とします. \( \lambda_i > 0 \) のとき, \( \lambda_i \) を \( \lambda \) の和因子といいます.

例えば, \( \lambda = (5, 4, 2) \) は 11 の分割（のひとつ）ですが, 4 は \(\lambda\) の和因子です.

定義：正の整数 \(n\) の分割の総数を \(p(n)\) で表し, これを\(n\) の分割数といいます.

例えば, 5 の分割は

5
4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1

の 7 通りあるので, \(p(5)=7\) です. なお, \(n\) の分割については,
入力された自然数の分割をすべて表示するプログラム
をチェックしてみるのも良いと思います.

ヤング図形と共役な分割

定義：\(\lambda = (\lambda_1, \lambda_2, \lambda_3, \cdots )\) を \(n\) の分割とします. \( \lambda \) のヤング図形とは, \(k\) 行目に \(\lambda_k\) 個のマス目を左端をそろえて並べたものです.

例えば, 11 の分割 \( \lambda = (5, 4, 2) \) のヤング図形は次のとおりです：

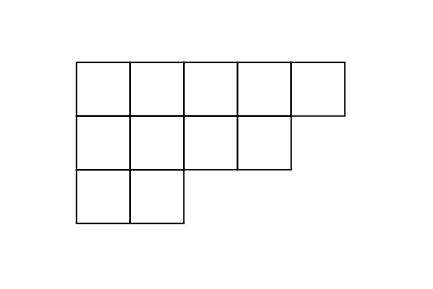
定義：\(\lambda = (\lambda_1, \lambda_2, \lambda_3, \cdots )\) を \(n\) の分割とします. 各正整数 \(i\) に対して, \( \lambda’_i \) を \( \lambda_k \geq i \) を満たすような \(k\) の個数とすると, \( \lambda’ = (\lambda’_1, \lambda’_2, \lambda’_3, \cdots) \) は \(n\) の分割となります. このとき, \( \lambda’ \) を \( \lambda \) の共役といいます.

例えば, 11 の分割 \( \lambda = (5, 4, 2) \) を考えたとき, 上の定義を踏まえると \( \lambda_1 = 5, \ \lambda_2 = 4, \ \lambda_3 = 2 \) であり,

1 以上の和因子は全部で 3 つなので \(\lambda’_1 = 3\)
2 以上の和因子は全部で 3 つなので \(\lambda’_2 = 3\)
3 以上の和因子は全部で 2 つなので \(\lambda’_3 = 2\)
4 以上の和因子は全部で 2 つなので \(\lambda’_4 = 2\)
5 以上の和因子は全部で 1 つなので \(\lambda’_5 = 1\)
6 以上の和因子は全部で 0 個なので \(\lambda’_6 = 0\)

であるので, \( \lambda’ = (3, 3, 2, 2, 1) \) は \( \lambda \) の共役となります.

注意：\( \lambda \) を \(n\) の分割とすると, \( \lambda \) の共役 \( \lambda’ \) のヤング図形は \( \lambda \) のヤング図形の行と列を入れ替えたものとなります.

例えば先ほどの例でいうと, \( \lambda = (5, 4, 2) \) の共役 \( \lambda’ = (3, 3, 2, 2, 1) \) のヤング図形は次のようになります.

定義：条件 \(P\) を満たすような \(n\) の分割の総数を \( p(n|P) \) と書くことにします.

\(k\) を正の整数とするとき, 共役をとることによって, 次が成り立つことがわかります.

\begin{align}
p(n|和因子は \ k \ 個) &= p(n|最大の和因子は \ k) \\
p(n|和因子は \ k \ 個以下) &= p(n | すべての和因子は \ k \ 以下)
\end{align}

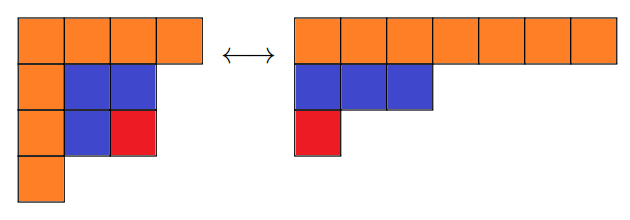
定義：\(n\) の分割 \( \lambda \) の共役が \( \lambda \) 自身と等しいとき, \( \lambda \) を \(n\) の自己共役な分割といいます.

\( p(n|分割は自己共役) = p(n|和因子は相異なる奇数) \) であることが知られています. 実際, 次のような一対一対応があります：

母関数

数列 \( a_0, a_1, a_2, a_3, \cdots \) があるとき,
\[
a_0 + a_1 q + a_2 q^2 + a_3 q^3 + \cdots
\] を数列 \( a_0, a_1, a_2, a_3, \cdots \) の母関数ということがあります.

それでは, 分割数 \(p(n)\) の母関数を求めてみましょう.
\begin{align}
& p(0) + p(1) q + p(2) q^2 + p(3) q^3 + \cdots \\
= {}& (1 + q^1 + q^{1 + 1} + q^{1 + 1 + 1} + \cdots)(1 + q^2 + q^{2 + 2} + q^{2 + 2 + 2} + \cdots)(1 + q^3 + q^{3 + 3} + q^{3 + 3 + 3} + \cdots)\cdots
\end{align} 例えば, この掛け算において \(q^4\) は,

\( q^4 \)
\( q^3 \cdot q^1 = q^{3 + 1} \)
\( q^{2 + 2} \)
\( q^2 \cdot q^{1 + 1} = q^{2 + 1 + 1} \)
\( q^{1 + 1 + 1 + 1}\)

で出てくるので, 確かに \( q^4 \) の係数は \(p(4)\) となっています. したがって,

\begin{align}
& p(0) + p(1) q + p(2) q^2 + p(3) q^3 + \cdots \\
= {}& \frac{1}{1-q^1} \cdot \frac{1}{1-q^2} \cdot \frac{1}{1-q^3} \cdots
\end{align}

となります（ただし \( |q| < 1 \) ）.

また, \( p(n|分割は自己共役) = p(n|和因子は相異なる奇数) \) なので,

\[
\sum_{n = 0}^{\infty} p(n|分割は自己共役) q^n = (1 + q^1)(1 + q^3)(1 + q^5)(1+q^7) \cdots
\]

が成り立ちます（ただし, ここでも \(q\) の範囲に注意する必要があります）.

オイラーの分割恒等式

定理（オイラーの分割恒等式）：
\[
p(n|和因子はすべて奇数)=p(n|和因子は相異なる)
\]

定理の証明に入る前に, \( n = 5 \) の場合についてチェックしてみましょう. 5 の分割は

5
4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1

の 7 通りありますが, このうち和因子がすべて奇数となるものは

5
3 + 1 + 1
1 + 1 + 1 + 1 + 1

の 3 通りです. 一方, 和因子が相異なるものは

5
4 + 1
3 + 2

の 3 通りなので, 確かに \(p(5|和因子はすべて奇数)=p(5|和因子は相異なる)\) が成り立っています.

では, 定理の証明に入りたいと思います. ここではオイラーによる証明を紹介します.

証明：母関数の比較による.
\begin{align}
\sum_{n = 0}^{\infty} p(n | 和因子は相異なる) q^n &= (1 + q^1)(1 + q^2)(1+ q^3)(1+q^4)\cdots \\
&= \frac{1-q^2}{1-q^1} \cdot \frac{1-q^4}{1-q^2} \cdot \frac{1-q^6}{1-q^3} \cdot \frac{1-q^8}{1-q^4} \cdots \\
&= \frac{\bcancel{1-q^2}}{1-q^1} \cdot \frac{\bcancel{1-q^4}}{\bcancel{1-q^2}} \cdot \frac{\bcancel{1-q^6}}{1-q^3} \cdot \frac{\bcancel{1-q^8}}{\bcancel{1-q^4}} \cdots \\
&= \frac{1}{1-q^1} \cdot \frac{1}{1-q^3} \cdot \frac{1}{1-q^5} \cdot \frac{1}{1-q^7} \cdots \\
&= \sum_{n = 0}^{\infty} p(n | 和因子はすべて奇数 ) q^n
\end{align}