皆さん, こんにちは. 管理人です. 今回は
\[
\sum_{c \in \textrm{Conj}(S_n)} \textrm{sgn}(c) = p(n | 和因子は相異なる奇数)
\] という式を証明したいと思います. ここで, 条件 \(P\) に対し, \(p(n | P)\) は条件 \(P\) を満たすような \(n\) の分割の個数を意味します. なので, \(p(n | 和因子は相異なる奇数)\) は \(n\) の分割であってその和因子が相異なる奇数であるようなものの個数を意味します. また, 群 \(G\) に対して, \(\textrm{Conj}(G)\) で \(G\) の共役類全体の集合を表すものとします.
注意事項
証明に入る前に, いくつか注意事項を述べたいと思います.
まず, \(\sigma \in S_n\) が \(\sigma’ \in S_n\) と共役であるとき, ある \(\alpha \in S_n\) が存在して \(\sigma = \alpha \sigma’ \alpha^{-1}\) が成り立ちます. よって, このとき
\[
\textrm{sgn}(\sigma) = \textrm{sgn}(\alpha \sigma’ \alpha^{-1}) = \textrm{sgn}(\alpha) \cdot \textrm{sgn}(\sigma’) \cdot \textrm{sgn}(\alpha^{-1}) = \textrm{sgn}(\sigma’)
\] となります. よって, 対称群 \(S_n\) の共役類 \(c\) の符号というものを考えることができます. つまり, 任意の \(c \in \textrm{Conj}(S_n)\) に対して, 代表元 \(\sigma \in c\) をひとつとって \(\textrm{sgn}(c) = \textrm{sgn}(\sigma)\) と定義すると, この定義は well-defined です.
ここで, \(S_n\) の共役類 \(c \in \textrm{Conj}(S_n)\) のサイクルタイプを \([l_1, l_2, \cdots, l_s] \) とします. 長さ \(k\) の巡回置換 \((\alpha_1, \alpha_2, \cdots, \alpha_k) \) について,
\[
(\alpha_1, \alpha_2, \cdots, \alpha_k) = (\alpha_1, \alpha_k)(\alpha_1, \alpha_{k-1})\cdots(\alpha_1, \alpha_3)(\alpha_1, \alpha_2)
\] が成り立つので,
\[
\textrm{sgn}(\alpha_1, \alpha_2, \cdots, \alpha_k) = (-1)^{k-1}
\] となります. ゆえに,
\[
\textrm{sgn}(c) = (-1)^{l_1-1}(-1)^{l_2-1}\cdots(-1)^{l_s-1}
\] となります.
証明
次のような母関数を考えます:
\[
F(q) = 1 + \sum_{n = 1}^{\infty} \left( \sum_{c \in \textrm{Conj}(S_n)} \textrm{sgn}(c) \right) q^n.
\] さて, \(F(q)\) の定義より,
\begin{align}
F(q) &= 1 + \sum_{n = 1}^{\infty} \sum_{\substack{s \geq 1, \\ l_1 \geq \cdots \geq l_s, \\ l_1 + \cdots + l_s = n}} (-1)^{l_1-1} \cdots (-1)^{l_s-1} q^n \\
&= (1 + q^1+q^{1+1}+\cdots)(1-q^2+q^{2+2}-q^{2+2+2}+\cdots)(1+q^3+q^{3+3}+\cdots)(1-q^4+q^{4+4}-q^{4+4+4}+\cdots)\cdots \\
&= \frac{1}{1-q^1} \cdot \frac{1}{1+q^2} \cdot \frac{1}{1-q^3} \cdot \frac{1}{1+q^4} \cdot \frac{1}{1-q^5} \cdot \frac{1}{1+q^6} \cdots
\end{align} となります. ここで,
\begin{align}
(1 + q^1)(1 + q^2)(1+ q^3)(1+q^4)\cdots
&= \frac{1-q^2}{1-q^1} \cdot \frac{1-q^4}{1-q^2} \cdot \frac{1-q^6}{1-q^3} \cdot \frac{1-q^8}{1-q^4} \cdots \\
&= \frac{\bcancel{1-q^2}}{1-q^1} \cdot \frac{\bcancel{1-q^4}}{\bcancel{1-q^2}} \cdot \frac{\bcancel{1-q^6}}{1-q^3} \cdot \frac{\bcancel{1-q^8}}{\bcancel{1-q^4}} \cdots \\
&= \frac{1}{1-q^1} \cdot \frac{1}{1-q^3} \cdot \frac{1}{1-q^5} \cdot \frac{1}{1-q^7} \cdots \\
\end{align} なので,
\begin{align}
F(q) &= (1+q^1)(1+q^3)(1+q^5)(1+q^7)\cdots \\
&= 1 + \sum_{n = 1}^{\infty} p(n | 和因子は相異なる奇数) q^n
\end{align} となります. 以上により,
\[
\sum_{c \in \textrm{Conj}(S_n)} \textrm{sgn}(c) = p(n | 和因子は相異なる奇数)
\] という式が成り立つことが証明されました.
余談
なお, \(p(n | 和因子は相異なる奇数) = p(n | 分割は自己共役) \) という式が知られています. 詳しくは
整数の分割
の「ヤング図形と共役な分割」を参照して下さい.
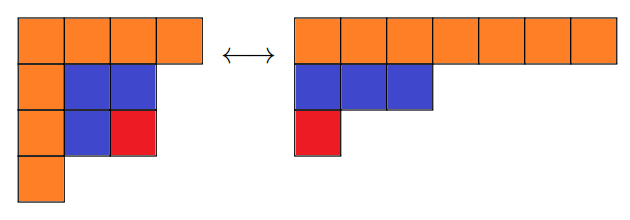
コメント