In this post, I will prove that
\[
\sum_{c \in \textrm{Conj}(S_n)} \textrm{sgn}(c) = \textrm{The number of partitions of \(n\) into distinct odd parts}
\] where \(n\) is a positive integer.
Notes
If \(\sigma \in S_n\) and \(\sigma’ \in S_n\) are conjugate, it holds that \(\textrm{sgn}(\sigma) = \textrm{sgn}(\sigma’). \) Therefore, we can define the sign of a conjugacy class of \(S_n\) as follows: let \(c\) be a conjugacy class of \(S_n\), then
\[
\textrm{sgn}(c) := \textrm{sgn}(\sigma)
\] where \(\sigma \in c\). This definition is well defined.
Let \(c\) be a conjugacy class of \(S_n\) and \((l_1, l_2, \cdots, l_s)\) be the cycle type of \(c\). Since a cycle \((\alpha_1 \ \alpha_2 \ \cdots \ \alpha_k)\) can be written as the product of \(k-1\) transpositions, i.e.,
\[
(\alpha_1 \ \alpha_2 \ \cdots \ \alpha_k) = (\alpha_1 \ \alpha_k)(\alpha_1 \ \alpha_{k-1}) \cdots (\alpha_1 \ \alpha_3)(\alpha_1 \ \alpha_2),
\] the sign of \((\alpha_1 \ \alpha_2 \ \cdots \ \alpha_k)\) is \((-1)^{k-1}\), i.e.,
\[
\textrm{sgn}((\alpha_1 \ \alpha_2 \ \cdots \ \alpha_k)) = (-1)^{k-1}.
\] Therefore, the sign of \(c\) is \((-1)^{l_1-1} (-1)^{l_2-1} \cdots (-1)^{l_s-1}\).
Proof
We can prove the beginning equation by using generating functions. Let
\[
F(q) = 1 + \sum_{n = 1}^{\infty} \left( \sum_{c \in \textrm{Conj}(S_n)} \textrm{sgn}(c) \right) q^n.
\] Then,
\begin{align}
F(q) &= 1 + \sum_{n = 1}^{\infty} \sum_{\substack{s \geq 1, \\ l_1 \geq \cdots \geq l_s, \\ l_1 + \cdots + l_s = n}} (-1)^{l_1-1} \cdots (-1)^{l_s-1} q^n \\ \\
&= (1 + q^1+q^{1+1}+\cdots)(1-q^2+q^{2+2}-q^{2+2+2}+\cdots)(1+q^3+q^{3+3}+\cdots)(1-q^4+q^{4+4}-q^{4+4+4}+\cdots)\cdots \\
&= \frac{1}{1-q^1} \cdot \frac{1}{1+q^2} \cdot \frac{1}{1-q^3} \cdot \frac{1}{1+q^4} \cdot \frac{1}{1-q^5} \cdot \frac{1}{1+q^6} \cdots.
\end{align} Since it holds that
\begin{align}
(1 + q^1)(1 + q^2)(1+ q^3)(1+q^4)\cdots
&= \frac{1-q^2}{1-q^1} \cdot \frac{1-q^4}{1-q^2} \cdot \frac{1-q^6}{1-q^3} \cdot \frac{1-q^8}{1-q^4} \cdots \\
&= \frac{\bcancel{1-q^2}}{1-q^1} \cdot \frac{\bcancel{1-q^4}}{\bcancel{1-q^2}} \cdot \frac{\bcancel{1-q^6}}{1-q^3} \cdot \frac{\bcancel{1-q^8}}{\bcancel{1-q^4}} \cdots \\
&= \frac{1}{1-q^1} \cdot \frac{1}{1-q^3} \cdot \frac{1}{1-q^5} \cdot \frac{1}{1-q^7} \cdots,
\end{align} it holds that
\begin{align}
F(q) &= (1+q^1)(1+q^3)(1+q^5)(1+q^7)\cdots \\
&= 1 + \sum_{n = 1}^{\infty} (\textrm{The number of partitions of \(n\) into distinct odd parts}) q^n.
\end{align} This completes the proof.
Digression
It is known that the number of partitions of \(n\) into distinct odd parts is the number of self-conjugate partitions of \(n\). This is because there is a following bijection.
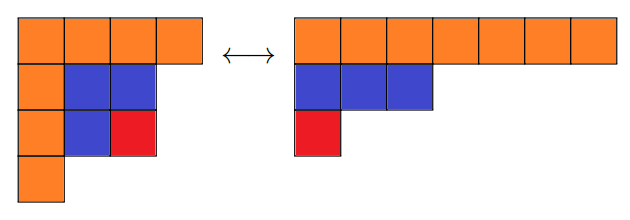
コメント